Ricerca Music Transcription

Music Transcription

Event Based Transcription System for Polyphonic Piano Music
Giovanni Costantini1,2, Renzo Perfetti4, Massimiliano Todisco1,3, 
1 Department of Electronic Engineering, University of Rome “Tor Vergata”, Rome, Italy
2 IDASC Institute of Acoustics and Sensors “Orso Mario Corbino”, Rome, Italy
3 Fondazione “Ugo Bordoni”, Rome, Italy
4 Department of Electronic and Information Engineering, University of Perugia, Perugia, Italy

Introduction
Music transcription can be considered as one of the most demanding activities performed by our brain; not so many people are able to easily transcribe a musical score starting from audio listening, since the success of this operation depends on musical abilities, as well as on the knowledge of the mechanisms of sounds production, of musical theory and styles, and finally on musical experience and practice to listening.
In fact, be necessary discern two cases in what the behavior of the automatic transcription systems is different: monophonic music, where notes are played one-by-one and polyphonic music, where two or several notes can be played simultaneously.
Currently, automatic transcription of monophonic music is treated in time domain by means of zero-crossing or auto-correlation techniques and in frequency domain by means of Discrete Fourier Transform (DFT) or cepstrum. With these techniques, an excellent accuracy level has been achieved.
Attempts in automatic transcription of polyphonic music have been much less successful; actually, the harmonic components of notes that simultaneously occur in polyphonic music significantly obfuscate automated transcription. The first algorithms were developed by Moorer, Piszczalski e Galler. Moorer (1975) used comb filters and autocorrelation in order to perform transcription of very restricted duets.
The most important works in this research field is the Ryynanen and Klapuri transcription system and the Sonic project developed by Marolt, particularly this project makes use of classification-based approaches to transcription based on neural networks.
The target of our work dealt with the problem of extracting musical content or a symbolic representation of musical notes, commonly called musical score, from audio data of polyphonic piano music.

Onset Detection
The aim of note onset detection is to find the starting time of each musical note. Several different methods have been proposed for performing onset detection [7, 8]. Our method is based on STFT and, notwithstanding its simplicity, it gives better or equal performance compared to other methods [7, 8].
To demonstrate the performance of our onset detection method, let us show an example from real piano polyphonic music of Mozart’s KV 333 Sonata in B-flat Major, Movement 3, sampled at 8 KHz and quantized with 16 bits. We will consider the second and third bar at 120 metronome beat. It is shown in Fig. 1.
We use a Short Time Fourier Transform (STFT) with N=512, an N-point Hanning window and a hop size h=256 corresponding to a 32 milliseconds hop between successive frames.
Figure 2 shows the onset detection function.

Mozart's KV 333 Sonata in B-flat MajorMozart_KV_333_Sonata_in_B-flat_Major
Fig. 1: Musical score of Mozart’s KV 333 Sonata in B-flat Major.

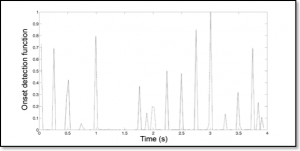
onset-detection-function
Fig. 2: Onset detection function for the example in Fig. 1

Spectral Features
In our work, the processing phase starts in correspondence to a note onset. Notice that two or more notes belong to the same onset if these notes are played within 32ms. Firstly, the attack time of the note is discarded (in case of the piano, the longest attack time is equal to about 32ms). Then, after a Hanning windowing, as single Constant Q Transform (CQT) of the following 64ms of the audio note event is calculated. Fig. 3 shows the complete process.

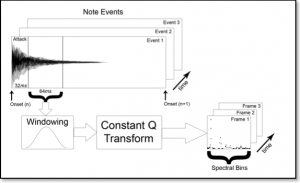
spectral-features
Fig. 3: Spectral features extraction

Multi-Class SVM Classification
A SVM identifies the optimal separating hyperplane (OSH) that maximizes the margin of separation between linearly separable points of two classes. In this context, the one-versus-all (OVA) approach has been used. The OVA method constructs N SVMs, N being the number of classes. The ith SVM is trained using all the samples in the ith class with a positive class label and all the remaining samples with a negative class label. Our transcription system uses 84 OVA SVM note classifiers. The presence of a note in a given audio event is detected when the discriminant function of the corresponding SVM classifier is positive. The SVMs were implemented using the software SVMlight, developed by Joachims. Fig. 4 shows a schematic view of the complete automatic transcription process.

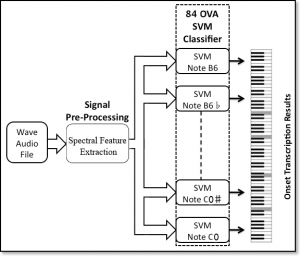
Automatic_Music_Transcription_System
Fig. 4: Schematic view of the complete automatic transcription process

Piano transcription example
We show now a specific example of piano music transcription concerning Johann Freidrich Burgmüller, The Fountain. We consider the fourth fifth and sixth bar at 60 metronome beat. The notes of these three bars have a wide range pitch (from G2 to A5) and duration (from 0.125s to 2s). In this example all 63 notes were successfully detected. In Figs. 6-8 the original piano score, the original midi piano roll and the transcription result midi piano roll are shown. We note some differences between the original and transcribed piano roll, mainly for the offset time, but this not affects the quality of the reconstruction.
Finally, you can hear the difference between the original score and transcription results.

Chopin_Opus_10_n.1
Fig. 6

Original_Chopin_Opus_10_n.1
Fig. 7

Transcription_Chopin_Opus_10_n.1
Fig. 8

Listen here

Chopin Opus 10, n. 1 Original score

Chopin Opus 10, n. 1 Transcription results

If you have any question, feedback or suggestion please don’t hesitate to contact us.

References

  1. G. Costantini, M. Todisco, G. Saggio, A New Method for Musical Onset Detection in Polyphonic Piano Music, 14th WSEAS International Conference on CIRCUITS, SYSTEMS COMMUNICATIONS and COMPUTERS, Corfu Island, Greece, July 22-25, 2010.
  2. G. Costantini, M. Todisco, R. Perfetti, Roberto Basili, SVM Based Transcription System with Short-Term Memory Oriented to Polyphonic Piano Music, 15th MELECON IEEE Mediterranean Electrotechnical Conference, Valletta, Malta, April 26-28, 2010, pp. 196-201.
  3. G. Costantini, M. Todisco, R. Perfetti, R. Basili, Memory Based Automatic Music Transcription System for Percussive Pitched Instruments, IMCIC International Multi-Conference on Complexity, Informatics and Cybernetics, Orlando, Florida, USA, April 6-9, 2010.
  4. G. Costantini, M. Todisco, R. Perfetti, R. Basili, Short-Term Memory and Event Memory Classification Systems for Automatic Polyphonic Music Transcription, 8th WSEAS International Conference on CIRCUITS, SYSTEMS, ELECTRONICS, CONTROL & SIGNAL PROCESSING, Puerto De La Cruz, Canary Islands, Spain, December 14-16, 2009, pp. 128-132.
  5. G. Costantini, M. Todisco, R. Perfetti, On the Use of Memory for Detecting Musical Notes in Polyphonic Piano Music, 19th ECCTD IEEE European Conference on Circuit Theory and Design, Antalya, Turkey, August 23-27, 2009, pp. 806-809.
  6. G. Costantini, M. Todisco, R. Perfetti, A Novel Sensor Interface for Detecting Musical Notes of Percussive Pitched Instruments, 3rd IWASI IEEE International Workshop on Advances in Sensors and Interfaces, Trani (Bari), Italy, June 25-26, 2009, pp. 121-126.
  7. G. Costantini, M. Todisco, R. Perfetti, Transcription of polyphonic piano music by means of memory-based classification method, 9th WIRN Italian Workshop on Neural Networks, Vietri sul Mare (Salerno), Italy, May 28-30, 2009.
  8. G. Costantini, R. Perfetti, M. Todisco, Event Based Transcription System for Polyphonic Piano Music, ELSEVIER, Signal Processing, Volume 89, Issue 9, September 2009, pp. 1798-1811.
  9. G. Costantini, M. Todisco, M. Carota, Improving Piano Music Transcription by Elman Dynamic Neural Networks, Proceedings of the 14th AISEM Italian Conference Sensors and Microsystems, Pavia, Italy, February 24-26, 2009.
  10. G. Costantini, M. Todisco, M. Carota, D. Casali, Static and Dynamic Classification Methods for Polyphonic Transcription of Piano Pieces in Different Musical Styles, Proceedings of the 12th WSEAS International Conference on CIRCUITS, SYSTEMS COMMUNICATIONS and COMPUTERS, Heraklion, Crete Island, Greece, July 22-24, 2008, pp. 158-162.
  11. J. A. Moorer, On the Transcription of Musical Sound by Computer, Computer Music Journal, Vol. 1, No. 4, Nov. 1977.
  12. M. Piszczalski and B. Galler, Automatic Music Transcription, Computer Music Journal, Vol. 1, No. 4, Nov. 1977.
  13. M. Ryynanen and A. Klapuri, Polyphonic music transcription using note event modeling, in Proceedings of IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA ’05), New Paltz, NY, USA, October 2005.
  14. M. Marolt, A connectionist approach to automatic transcription of polyphonic piano music, IEEE Transactions on Multimedia, vol. 6, no. 3, 2004.
  15. J. C. Brown, Calculation of a constant Q spectral transform, Journal of the Acoustical Society of America, vol. 89, no. 1, pp. 425–434, 1991.
  16. J. Shawe-Taylor, N. Cristianini, An Introduction to Support Vector Machines, Cambridge University Press (2000).
  17. G. Poliner and D. Ellis, A Discriminative Model for Polyphonic Piano Transcription, EURASIP Journal of Advances in Signal Processing, vol. 2007, Article ID 48317, pp. 1-9, 2007.

 

 

I commenti sono chiusi